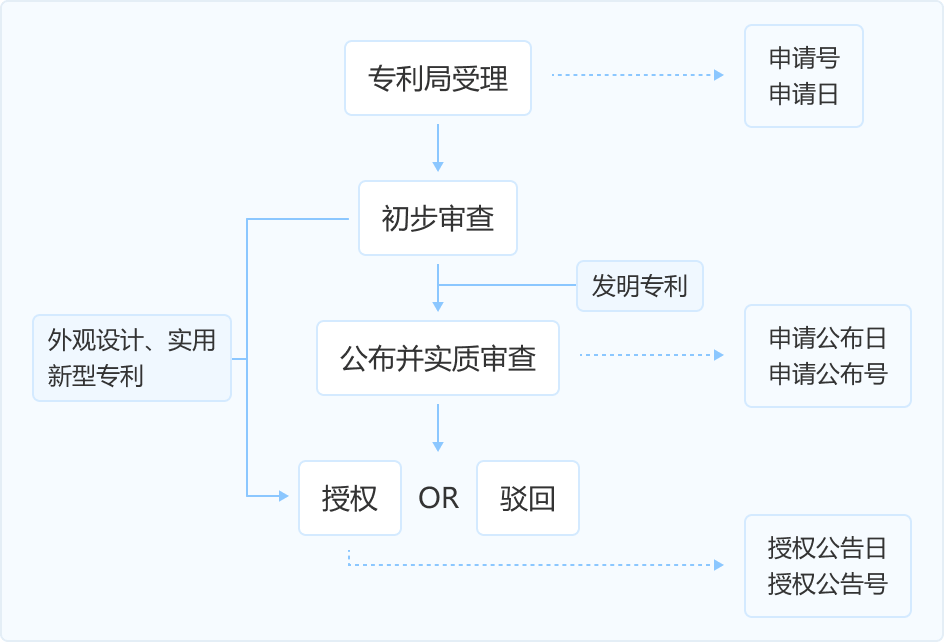
[0033] 参见图1,所示为本发明一种两轮自平衡机器人滑模自适应控制系统的原理框图,包括传感器测量模块、主控芯片、通讯模块、转向杆线性霍尔传感器和电机系统,其中,传感器测量模块采用于集自平衡机器人运动参数,至少包括陀螺仪和加速度计,分别用于采集角速度信号和加速度信号,其中,陀螺仪的型号为L3G420D,加速度计的型号为LSM303D;电机系统用于驱动两轮自平衡机器人运动,电机系统为两轮自平衡机器人的动力执行系统,至少包括无刷电机及其驱动电路;通讯模块采用串口通信模块或者无线数据传输模块,用于与外部设备进行数据通讯,以便于系统调试和维修检测;转向杆线性霍尔传感器用于实现自平衡机器人转向控制;主控芯片与传感器测量模块和电机系统相连接,用于根据所述传感器测量模块采集的运动参数控制所述电机系统的运动;进一步的,主控芯片采用DSP芯片,在其中设置滑模自适应控制器,参见图2,所示为本发明中滑模自适应控制器的原理框图,其中,滑模自适应控制器的输出方程为:
[0034] U=-(K+φ)X;
[0035] 其中,滑模自适应控制器根据实时输入的角度参量θ和角速度 控制输出电压U从而驱动电机系统运动;电机系统运动使角度参量θ和角速度 发生改变并反馈至滑模自适应控制器,从而运动参数的反馈量可以调节输出电压U,并不断循环该过程,使两轮自平衡机器人能够最大程度降低外界环境中各种干扰。
[0036] 上式中,X为角度参量θ和角速度 的集合,K是通过极点计算出来的参数矩阵;φ取值是根据以下公式决定:
[0037] γ是自适应速率,e为角度误差参数,C取[0 0 1 1]。
[0038] 上述滑模自适应控制器的设计原理如下:
[0039] 两轮自平衡机器人的系统可以等效看作是一个倒立摆模型,参见图3,所示的倒立摆模型结构为现有技术通用的动力模型。从能量和动量角度分析,利用拉格朗日动力学理论,可以得到以下描述:
[0040]
[0041] U=-mgl+mgl cosθ (2)
[0042] (2)式中,U为电动机输出电压,电动机施加电压后会产生力矩,该力矩与平衡车运动的势能成正比关系。
[0043] (1)式和(2)式中,m为车身质量,Mw为转子(轮胎)质量,l为摆杆长度、Je为平衡车转动惯量、Jm为转子(轮胎)转动惯量, 平衡车轮胎转速,R为平衡车轮胎半径,这些参量都为自平衡机器人的固有参量,取决于自平衡机器人机械架构;在倒立摆模型下的不同机械架构,上述参量会发生变化。
[0044] 其中,Xw为路程、 为速度、θ为角度和 为角速度为自平衡机器人的运动参量,这些数据可以通过传感器采集到。
[0045] 在两轮自平衡机器人控制中,θ变化范围很小所以cosθ可以近似为1,sinθ可以近似为θ,然后根据(1)、(2)两个方程联立可以得到:
[0046]
[0047]
[0048] 写成状态空间形式:
[0049]
[0050] 然后我们可以另于是动力学模型可简化为
[0051]
[0052] 即简写形式:
[0053]
[0054] 由公式(7)可以选择合适的系统控制极点设计出控制器(一般p=[v1,v2,v3,v4],v1,v2,v3,v4<0利用matlab中place函数计算出K,K=place(A,B,p)),从而得到下式:
[0055] U=-K·X (8)
[0056] 其中,K是通过选择合适极点计算出来的参数矩阵,X为
[0057] 式(8)的控制器输出方程能够很好的实现直立自平衡,并且在控制精度上远优于PD控制,在极端情况中不易失控,但这个控制器缺少对外界条件的适应力,因此,本发明在此基础上还对控制器进行进一步优化。
[0058] 为了提高控制器的自适应能力,根据滑模控制理论在控制器加入滑模参量。滑模的最大优点在于鲁棒性强并且对于外界条件变化引起的参数摄动具有很强的免疫力。于是将控制器设计为:
[0059] U=-(K+φ)X (9)
[0060] 其中K=[k1 k2 k3 k4],φ=[φ1 φ2 φ3 φ4],φ取值是根据以下公式决定:
[0061]
[0062] 滑模参量φ会根据实际采集值与误差进行不断累加和更新,当控制力度不足或过度时φ就会发生变化增大或减少,从而一直保持控制器输出最优结果,从而实现对参数摄动的抵抗作用。其中,sign为符号函数,γ是自适应速率,为常量,实际调试中选取合适值;e为角度误差参数,采集角度和期望角度的差值。
[0063] 为了使控制器输出方程稳定,必须符合李雅普诺夫稳定性原理,证明如下:
[0064] (7)式动力学方程可简化为:
[0065]
[0066] Y=C·X (11)
[0067] 将重新设计的控制器(9)式代入动力学方程,可以得到:
[0068]
[0069] Y=C·X (12)
[0070] 其中v为控制器输入向量。
[0071] 定义矩阵P,若存在矩阵Q满足ATP+PA=-Q,PB=C,C取[0 0 1 1],这里只要满足矩阵A是满秩,就可以证明Q存在。通过Matlab计算出r(A)=4。
[0072] 由此可见矩阵A为满秩矩阵。然后构造能量函数:
[0073]
[0074] 对V求导并代入(11)式与(13)式可得:
[0075]
[0076] 由此证明了该控制器满足李雅普诺夫稳定性原理。
[0077] 通过上述技术方案,显著提高了自适应能力,但对在使用过程中的长期变化会每次都重新匹配,比如两轮自平衡机器人的机械特性或人为的操作习惯,无法智能匹配。
[0078] 为了解决上述技术问题,本发明根据机器学习的理论,对两轮自平衡机器人的控制器进行进一步优化使其能够适应人的各种习惯,在滑模自适应控制器中设置机器学习表(Map),机器学习表(Map)是在出厂时根据运行环境和驾驶习惯针对各种输入的角度参量θ和角速度 调试出来的一张参数表,在实际运行中,能够根据输入的角度参量θ和角速度在Map表中查找所对应的参数值,从而能够调节输出电压U。
[0079] 在一种优选实施方式中,滑模自适应控制器还包括机器学习模块,机器学习模块用于根据输入的角度参量θ和角速度 更新机器学习表(Map),从而使机器学习表(Map)中的参数始终保持最优值,从而能够适应人的各种习惯。
[0080] 由此,控制器的输出方程如下:
[0081] U=-(K+φ)X+Map(X) (16)
[0082] 式(16)是在(9)式控制器输出方程的基础上进行扩展,其中Map(X)是通过机器学习的方法对控制器进行优化的参数表。该优化主要针对两轮自平衡机器人系统在实际情况中的非线性因素,例如人的主观控制,从而改善驾驶操控。
[0083] 该控制器前段已在之前通过稳定性证明,只需要证明后端,定义能量函数:
[0084]
[0085] 求导后得到:
[0086]
[0087] 其中Xb=Y=CX
[0088] 使用梯度优化法取:
[0089]
[0090] 这里ρ为梯度法步进,可以使 当e=0时取“=”。
[0091] Map本质上是一张查找表,该方法会对每一个X根据误差和能量进行单独修正,从而使控制器在运行时能量|L|能够收敛到区间(vmin,vmax)内从而使控制不会产生过度响应,实际调试中在平衡车加速和减速时,由于加速和减速不平滑因此会产生较大的|L|,该方法使直立车加减速平滑化,给人一种比较柔和的感觉尤其是在起步和停车过程中,这种感觉会更加明显。
[0092] 在一种优选实施方式中,主控芯片获取角速度信号和加速度信号,通过IMU算法计算出4元数,再通过4元数还原出三个方位的欧拉角。从而计算得到角度参量θ和角速度[0093] 参见图4,所述为本发明两轮自平衡机器人的系统执行流程图,通过传感器模块获取两轮自平衡机器人姿态,通过转向杆上的线性霍尔传感器获取转向期望信号,然后通过DSP芯片进行运算处理,分别计算出两只无刷电机的控制量,从而实现自平衡。在此同时本发明还将一些系统参数通过通讯模块发送出去,以便实时监测与观测。
[0094] 该系统在开始执行后首先进行初始化,然后分两条不同频率的任务,一条是方向控制,执行周期为20ms;另一条为本发明的平衡控制,执行周期为5ms。其中平衡控制首先通过传感器(陀螺仪和加速度计)采集角速度信号和加速度信号,然后通过姿态计算计算出两轮平衡车角度,然后根据角度计算出自适应律,并通过自适应控制器计算出自适应控制输出,接着根据Map查找出最优的Map输出,然后根据采集到的信号更新Map库,再将Map输出与自适应输出进行叠加从而计算出平衡控制输出,最后将直立控制和方向控制的控制输出进行叠加然后滤波从而控制电机输出。
[0095] 采用本发明的技术方案,能够对外界环境进行自适应同时能够最大程度降低外界环境中各种干扰对两轮平衡车的影响并且不损失鲁棒性,同时还能利用机器学习的方法对一些长期积累因素(如两轮平衡车的机械特性或人为的操作习惯)进行磨合最终使两轮平衡车具有优秀的性能。
[0096] 参见图5,所示为仿真运行一段时间后的机器学习库的状态图,其中仿真条件是在其输入信号加载峰峰值为1频率为3kHz的g高频扰动和幅度为0.01的噪声信号。在运行一段时间后,其运行时出现的每个角度与角速度状态都经过机器学习、更新演化出如图6所示的机器学习Map表,可以看出在经机器学习以后,Map表对改机器学习的高频扰动和噪声信号的反应更为均匀,从而实现对控制器进行进一步的优化。
[0097] 参见图6,所示为本发明在输入信号加载峰峰值为1频率为3kHz的g高频扰动和幅度为0.01的噪声信号仿真时的角度误差变化曲线,图7为在同样仿真条件下移除机器学习功能时的角度误差变化曲线,图8为在同样仿真条件下传统PID算法的角度误差变化曲线。从图6,图7和图8的仿真结果对比可以很明显的发现本发明的性能明显要优于传统PID算法,从图6和图7的对比,可以清楚的算出本发明中的机器学习模块可以对与控制中的细节部分进行进一步地改善从而增强了本发明的自适应控制性能。
[0098] 以上实施例的说明只是用于帮助理解本发明的方法及其核心思想。应当指出,对于本技术领域的普通技术人员来说,在不脱离本发明原理的前提下,还可以对本发明进行若干改进和修饰,这些改进和修饰也落入本发明权利要求的保护范围内。
[0099] 对所公开的实施例的上述说明,使本领域专业技术人员能够实现或使用本发明。对这些实施例的多种修改对本领域的专业技术人员来说将是显而易见的,本发明中所定义的一般原理可以在不脱离本发明的精神或范围的情况下,在其它实施例中实现。因此,本发明将不会被限制于本发明所示的这些实施例,而是要符合与本发明所公开的原理和新颖特点相一致的最宽的范围。